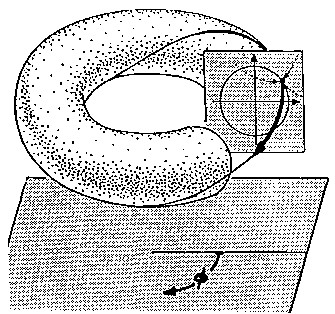
Cyclic motion of a system in two planes of the (at least three-dimensional) phase space generates a sort of bike tube as the attractor, i.e. a (two-dimensional) toroidal surface.

On the torus attractor, exact periodicity is not guaranteed in general. However, after a long enough wait the (quasiperiodic) system returns arbitrarily often and arbitrarily close to each point of the torus surface (recurrence). Closely neighbouring trajectories do not depart from each other. If one only observes the system's behaviour long enough, one may forecast its motion for every desired timespan, it remains predictable.

Imbedded in a sea of quasiperiodic orbits, though, lies even an infinite number of exactly periodic ones as well - namely those where minor and major revolutions exhibit integer mutual relationships.