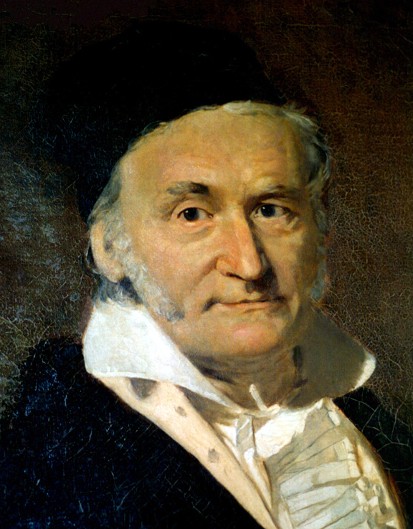Carl Friedrich Gauss is raised in humble circumstances and from an early age shows an exceptional gift for mathematics. He contributes pioneering work to nearly all areas of mathematics, also to astronomy and physics. Achievements in number theory and the calculation of the orbit of the small planet Ceres make him famous throughout Europe. At the age of thirty, Gauss is appointed director of the observatory in Göttingen, where he is active for more than forty years. There, he develops his ideas on non-Euclidean geometry, prompted by doubts about a possible proof of the parallel axiom of the Euclidean geometry, which states that parallel lines never cross. Around 1820, Gauss starts work on a large-scale geodesic survey. In connection with this project he works on a variety of mathematical problems. In particular, Gauss develops the basis of differential geometry of curved surfaces; a starting point for Einstein’s insight into the curvature of space and time.